高等数学(同济大学第七版)学习笔记-第二章-导数与微分

导数与微分

导数

导函数

特殊函数的导数公式

幂函数的导数公式

幂函数f(x) = xⁿ (n ϵ R ) 的导数公式：

(xⁿ)^‘ = nx^n-1

三角函数的导数公式

• 正弦函数 f(x) = sin x 的导数公式

  • (sin x)^‘ = cos x

  即正弦函数的导数是余弦函数。

• 余弦函数 f(x) = cos x 的导数公式：

  • (cos x)^‘ = -sina x

  即余弦函数的导数是负的正弦函数。

• 正切函数 f(x) = tan x 的导数公式：

  • (tan x)^‘ = sec²x

• 余切函数 f(x) = cot x 的导数公式：

  • (cot x)^‘ = - csc²x

• 正割函数 f(x) = sec x 的导数公式：

  • (sec x)^‘ = sec x * tan x

• 余割函数 f(x) = csc x 的导数公式：

  • (csc x)^‘ = - csc x * cot x

• 反正弦函数 f(x) = arcsinx x 的导数公式：

• 反余弦函数 f(x) = arccos x 的导数公式：

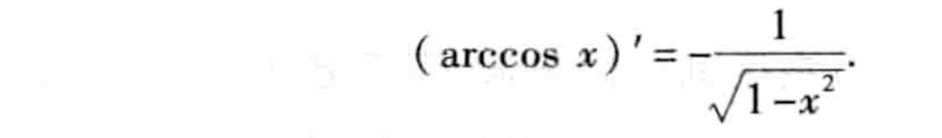
• 反正切函数 f(x) = arctan x 的导数公式：

• 反余切函数 f(x) = arccot x 的导数公式：

指数函数的导数公式

指数函数f(x) = a^x (a>0,a≠1)的导数公式:

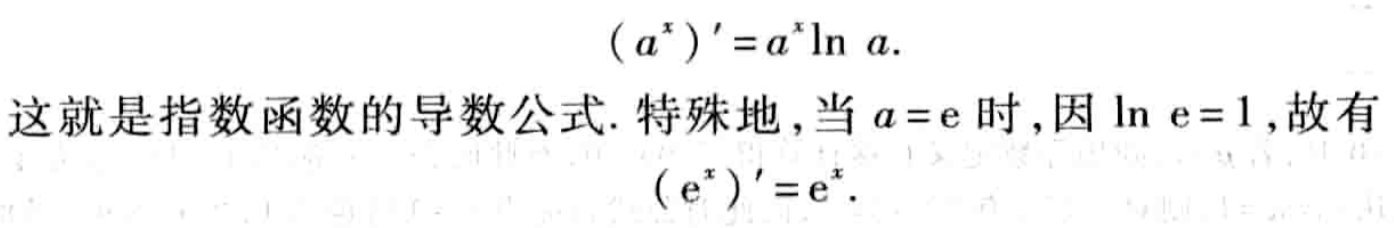
对数函数的导数公式

对数函数f(x) = log_ax (a>0,a≠1)的导数公式:

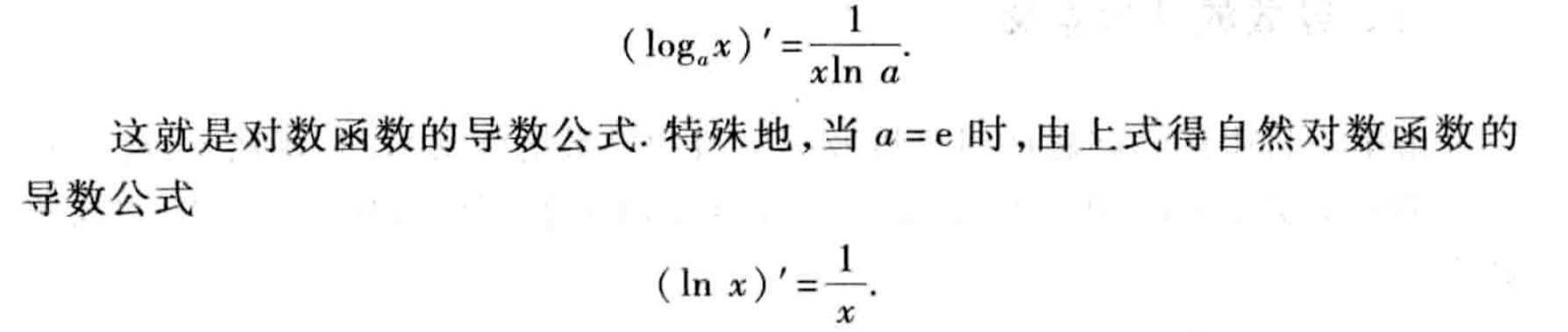
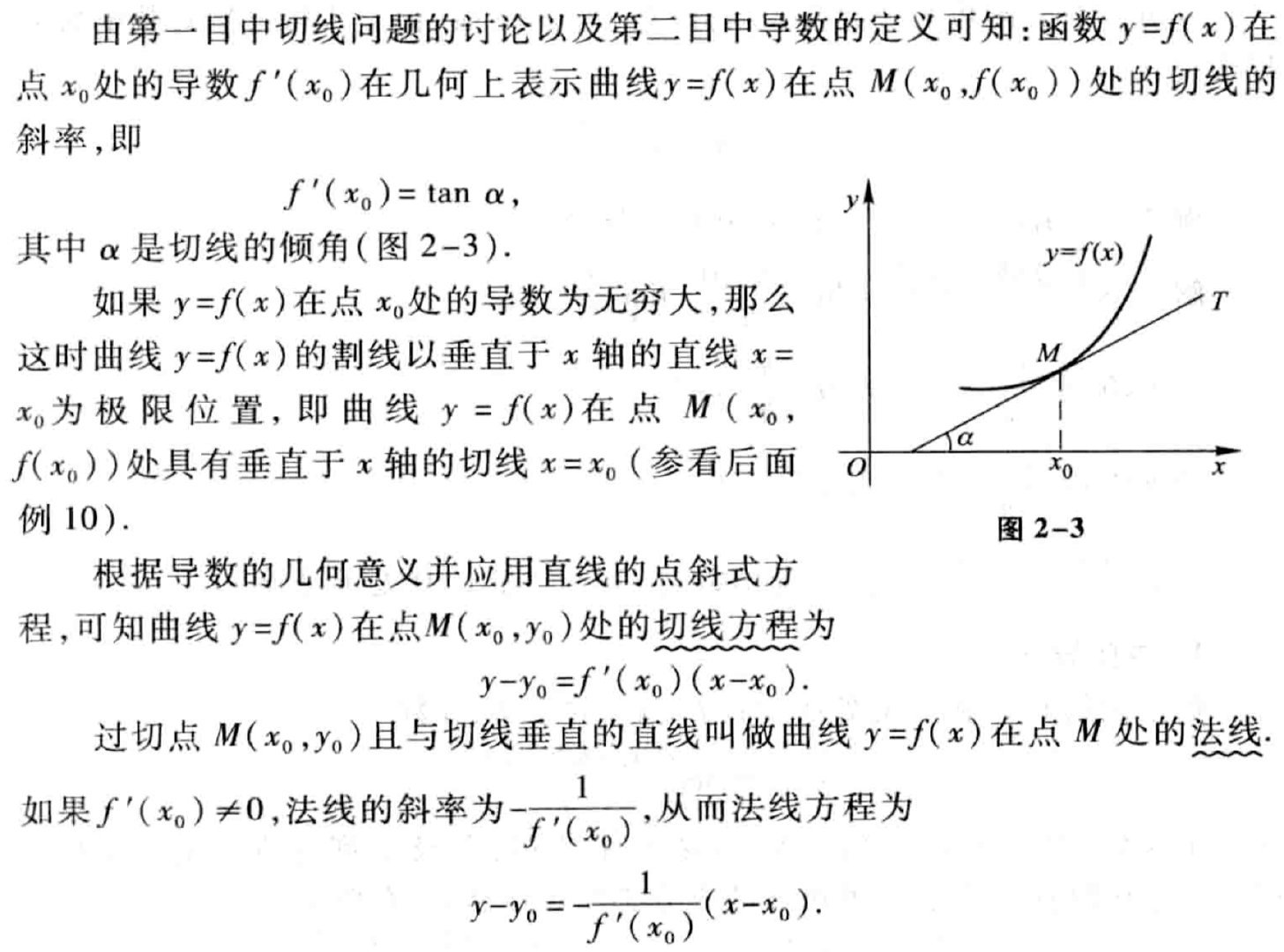
导数的几何意义

求导法则

函数的和，差，积，商的求导法则

反函数的求导法则

• 即反函数的导数等于直接函数导数的倒数。

复合函数的求导法则

基本初等函数的导数公式总结：

高阶导数

微分

微分的几何意义

基本初等函数的微分公式

函数和，差，积，商的积分法则

复合函数的微分法则

微分中值定理

费马引理

罗尔定理

拉格朗日中值定理

拉格朗日中值定理的几何意义

柯西中值定理

洛必达法则

泰勒公式

函数的单调性

曲线的凹凸性

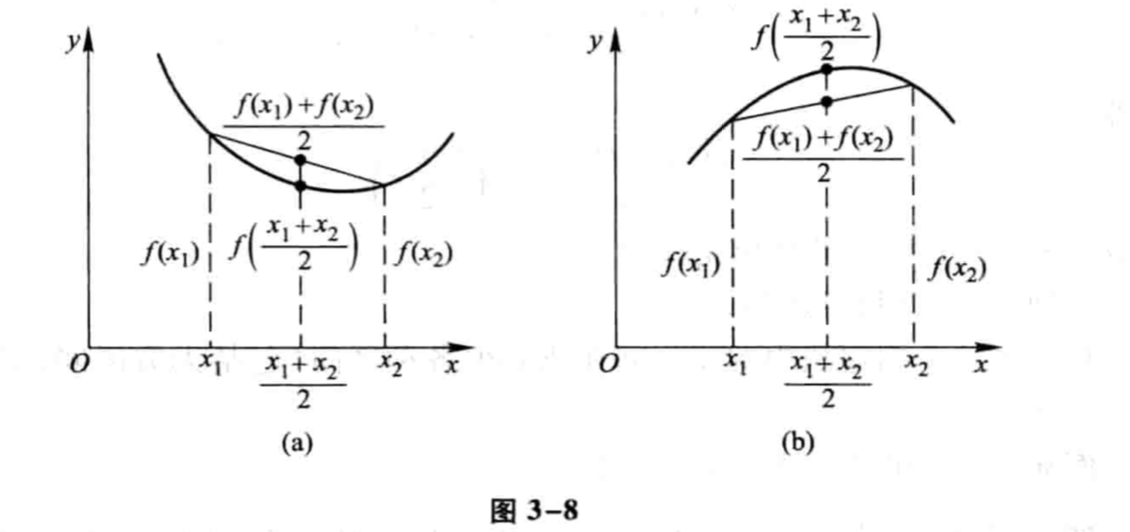
函数的极值与最大值最小值

• 当函数取极大值和极小值时，函数在这两个点的导数值等于0。

  • 当函数在该点的二阶导数为正时，函数取极小值。
  • 当函数在该点的二阶导数为负时，函数取极大值。
  • 当函数在该点的二阶导数为0时，该点称为函数的拐点。

• 微积分中的大部分问题，都可以令其导数值为0来求解。